Game Coordinate Spaces

When playing a computer game, we see the objects of our game world projected onto our screens. It’s easy to think these objects are just “placed” where they need to be in the screen, but game objects exist in many spaces, and are transformed between them until they reach their final position on the screen. In this article, I will go over these coordinate spaces, and how we transform objects to move between them.

Before we get started, I’d like to point out that I’ve borrowed some images for this article from learnopengl.com (please see attribution information at the bottom of the article). I highly, highly recommend anyone interested in game engine development to check out this site. You’ll find in-depth yet easy to understand tutorials on building games entirely with OpenGL. I have benefited immensely from it. If you’re interested in learning the math used in game development, you can’t go wrong with picking up a copy of 3D Primer for Graphics and Game Development. Check out the book’s website: gamemath.com.

What are Coordinate Spaces?

A coordinate system uses numbered coordinates to describe the exact position of a point in space. The points in this system define the position of our objects in virtual space. Objects move through spaces with transformation matrices, but I’ll delve more into that later.

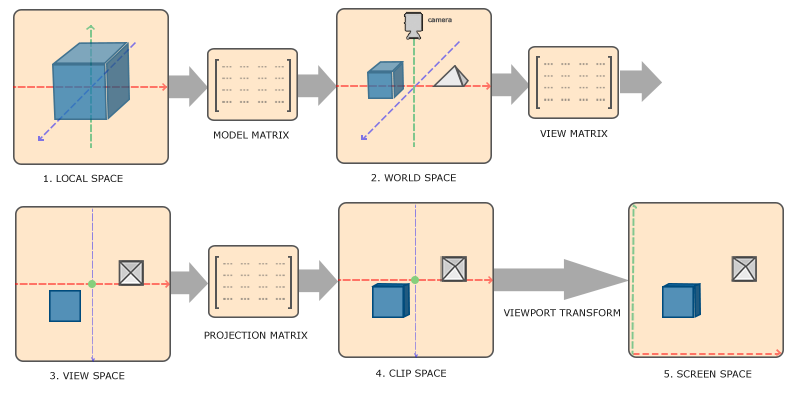
Below, I’ll go over each space that objects move through in the render pipeline until getting drawn on screen.

Local Space

Local space is also referred to as model space, or object space. All objects in local space are centered at the origin (0,0,0) of the coordinate system. The object does not exist relative to anything else; it is the only thing in this space.

World Space

World space is a global space defining the absolute position of objects relative to the world’s origin. For instance, an object’s position in world space may be (1,1,1). That is, shifted one unit along the x, y, and z axes. Remember, in local space, the object must always be centered at the origin. In world space, its coordinates could be anywhere relative to the origin.

View Space

This is also called camera, or eye space. In view space, the camera is at the origin of the coordinate system. The +z axis points away from the camera, opposite its view angle. The +y axis points up, not up in terms of our world, but up relative to the camera’s orientation. The +x axis juts out to the right from origin. I should point out that these are using the right-handed, OpenGL convention. In a left-handed convention, The +z axis would be pointing forwards into the view angle. Handedness is outside the scope of this article.

Clip Space

Clip space, or projection space, describe where objects reside after we have transformed view space using a projection matrix (more on that later). Clip space is surrounded by six “clip” planes. The near-clip plane is the plane on the view frustum closest to the camera along its forward (local z-axis) vector. The far clip plane is the plane at the farthest z-axis extent of the frustum. Anything in front of the near-clip plane, and anything behind the far-clip plane will not render to the screen. The remaining planes in the frustum are defined by these two. The x, y, and z components of the vertices in this space must be within the -1.0 ~ 1.0 range (for OpenGL). If they are not, they will be “clipped” out of the scene and will not render to the screen.

Projection

There are two main types of projection used in game development: perspective and orthographic.

Perspective Projection

Perspective projection is the most common of the two, because it mimics how we view the world ourselves. The lines connecting objects in space in perspective all converge to a single point. Objects in perspective are foreshortened based on their distance from the camera.

Orthographic Projection

In orthographic projection, the lines connecting objects are parallel. To the viewer, an object’s size does not change relative to its distance from the camera. So long as objects are within the range of projection, they will all render as their original size on screen.

Screen Space

The final destination of our objects is screen space. Screen space is the final rasterisation of vertices that were not clipped out in clip space, onto the screen. Screens only have width and height, so by nature screen space is 2D – it only has x and y components. The vertices of our objects are scaled to fit into the viewport of our screen. By this stage, our vertices aren’t really forming 3D “objects” anymore. Think of them more as 2D projected images on the screen. The interesting thing about screen space is that we don’t handle transformation to this space ourselves. Once we’re ready to convert to screen space, vertices are sent into the GPU, which in turn automatically transforms them to our viewport.

Matrix Transformations

Objects and vertices move between spaces with something called a transformation matrix. A matrix is simply an array, or table of numbers. The elements in the matrix all serve a specific function in transforming a point from one space to another. There are three basic type of transformation that occurs with these matrices: translation, rotation, and scale.

Translation is the movement of a point in space. Rotation is self explanatory: it rotates a point. Scale adjusts the size. Each of these transformations have their own 4x4 matrix, which are multiplied together to completely transform the point. Doing this will move the point into world space.

It’s worth noting that the order of multiplication for these transformation matrices matters. Depending on the graphics API you are using, this order changes. For Opengl, this is order is: translation, rotation, scale. It’s not intuitive, but when multiplying in code, you must pre-multiply in the opposite order.

world matrix = scale * rotation * translation;

Below are the transformation matrices described above. In this article, I use column-major matrices.

Translation Matrix

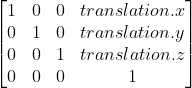
Notice that all the elements for translation are in the first three rows on last column. This is where they must be in OpenGL.

Scale Matrix

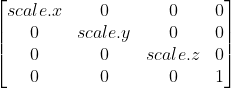
Rotation Matrix

Each axis of rotation has it’s own matrix, these need to be multiplied together to get the full rotation. Note that theta is the angle of rotation.

X-axis Rotation Matrix

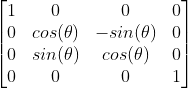
Y-axis Rotation Matrix

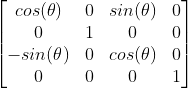
Z-axis Rotation Matrix

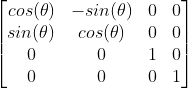
Once we’ve transformed the point to world space, we use something called the view matrix to convert the model to view space, and projection matrix to convert to clip space.

View Matrix

The view, or “look-at” matrix is what we use to convert world space to camera space. It takes three vectors: The “look-at” vector, or the direction along the camera’s forward axis. The camera’s up vector, and the right vector that juts out from the first two. Note that in OpenGL, you can use the gluLookAt API call to move a point into view space. Below is OpenGL’s look-at matrix:

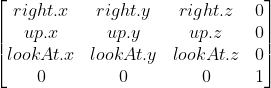
Projection Matrix

The last matrix transformation we do ourselves is from view to clip space. This is done with something called the projection matrix, or “clip” matrix. I described two common types of projection above: perspective and orthographic. These types each have their own projection matrix. What’s going on mathematically in these matrices is a bit complex, and outside the scope of this article. But you’ll notice they make use of the near and far values described above.

Perspective Projection Matrix

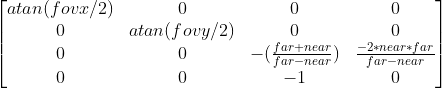
Orthographic Projection Matrix

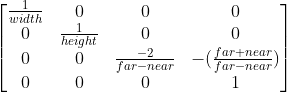
Conclusion

The best way to solidify you’re understanding of coordinate spaces and transformation matrices is to implement them yourself. Choose a graphics API such as Direct X or OpenGL (I recommend OpenGL), a language (C++ is good), a good tutorial (learnopengl.com), and give it a go!

Licensed Material Attribution

The images from learnopengl.com are compliant with the CC By 4.0 (https://creativecommons.org/licenses/by/4.0/) license agreement. Copyright, Joey de Vries (https://twitter.com/JoeyDeVriez). Site information: https://learnopengl.com/About.

[go to home page]